MỘT SỐ BÀI TOÁN VỀ DÃY CÁC PHÂN SỐ VIẾT THEO QUY LUẬT

Ta thường gặp một số bài toán trong đó các phân số có tử và mẫu được viết theo quy luật. Việc phát hiện ra quy luật viết của các phân số giúp ta tìm được cách giải nhanh chóng và thuận tiện.

1. Bài tập minh họa

Bài tập `1`:  Hãy tính tổng các phân số sau đây theo cách nhanh nhất

a) `A=1/1.2+1/2.3+...+1/2022.2023`

b) `B=2/(1.3) +2/(3.5)+2/(5.7)+...+2/(97.99)`

c) `C=3/28+3/70+3/130+...+3/550`

d) `D=4/(1.10) + 4/(10.19)+4/(19.28)+...+4/(82.91)`

Phân tích: Các phân số trong các bài tập này có thể đưa về dạng `a/(n(n+a)`

Đó là các phân số có tử không đổi và đúng bằng hiệu hai thừa số dưới mẫu. Và trong một tổng thì thừa số cuối ở mẫu của phân số trước bằng thừa số đầu ở mẫu của phân số sau. Nếu ta viết mỗi phân số dạng trên thành hiệu của hai phân số sao cho số trừ ở nhóm trước bằng số bị trừ ở nhóm sau thì ta có thể khử liên tiếp để thực hiện tính tổng một cách dễ dàng.

Công thức: `a/(n(n+a))=1/n - 1/(n+a)`

Chứng minh: `a/(n(n+a))=(n+a-n)/(n(n+a))=(n+a)/(n(n+a)) - n/(n(n+a))=1/n-1/(n+a)`

Ví dụ: `1/2.3=1/2 - 1/3;2/3.5=1/3-1/5;4/5.9=1/5-1/9`

Lưu ý: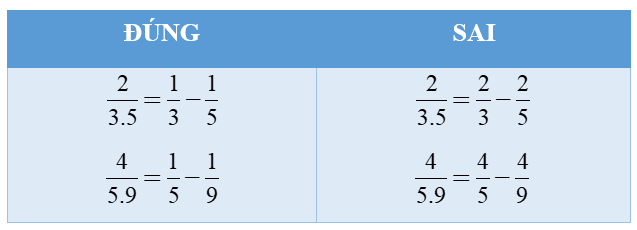 

Áp dụng công thức `a/(n(n+a))=1/n - 1/(n+a)` ta có thể tính các tổng đã cho như sau:

a) `A=1/1.2+1/2.3+...+1/2022.2023=1/1-1/2+1/2-1/3+...+1/2022 -1/2023=1-1/2023=2022/2023`

b) `B=2/(1.3) +2/(3.5)+2/(5.7)+...+2/(97.99)=1-1/3-1/3+1/3-1/5+1/5-1/7+...+1/97-1/99=1-1/99=98/99`

c) `C=3/28+3/70+3/130+...+3/550`

Nhận xét:  Ta thấy tử của các phân số bằng `3`, trong khi phần mẫu chưa được phân tích về dạng tích.

Do đó ta sẽ biến đổi để các mẫu số về dạng tích của hai thừa số có hiệu bằng `3`.

Nhận thấy:   `28=4.7;70=7.10;130=10.13;… ;550=22.25`

Do vậy:

`C=3/28+3/70+3/130+...+3/550`

`=3/(4.7)+3/(7.10)+3/(10.13)+...+3/(22.25)`

`=1/4-1/7+1/7-1/10+1/10-1/13+...+1/22-1/25`

`=1/4-1/25=21/100`

d) `D=4/(1.10) + 4/(10.19)+4/(19.28)+...+4/(82.91)`

Nhận xét:  Ta thấy ở mỗi phân số, hiệu của hai thừa số dưới mẫu bằng `9`. Trong khi đó các tử lại có giá trị bằng `4`.

Do đó ta sẽ biến đổi để cho tử số bằng `9` (đúng bằng hiệu hai thừa số dưới mẫu) như sau:

`D=4/(1.10) + 4/(10.19)+4/(19.28)+...+4/(82.91)`

`=4/9[9(1/(1.10) + 1/(10.19)+1/(19.28)+...+1/(82.91))]`

`=4/9(9/(1.10) + 9/(10.19)+9/(19.28)+...+9/(82.91))`

`=4/9(1-1/10+1/10-1/19+1/19-1/28+...+1/82-1/91)`

`=4/9(1-1/91)=4/9 . 90/91=40/91`

Bài tập `2`: Tính nhanh: `A=1/2 + 1/2^2+1/2^3+1/2^4+...+1/2^10`

Phân tích:
Ta nhận thấy kể từ số hạng thứ hai, mỗi phân số bằng phân số đứng ngay trước nó nhân với `1/2`. Do đó nếu nhân 2 vào tổng A, ta sẽ tạo ra được một tổng mới có nhiều số hạng giống tổng ban đầu.

Lời giải:

`A=1/2 + 1/2^2+1/2^3+1/2^4+...+1/2^10`           `(1)`

`2A=1+1/2 + 1/2^2+1/2^3+...+1/2^9`              `(2)`

Lấy `(2)` trừ `(1)` ta có:

`2.A-A=(1+1/2 + 1/2^2+1/2^3+...+1/2^9)-(1/2 + 1/2^2+1/2^3+1/2^4+...+1/2^10)`

`=> A=1+1/2 + 1/2^2+1/2^3+...+1/2^9-1/2 - 1/2^2-1/2^3-1/2^4-...-1/2^10`

`=> A=1-1/2^10=1-1/1024=1023/1024`

Bài tập `3:` Tìm tích của `98` số đầu tiên trong dãy `1 1/3; 1 1/8;1 1/15; 1 1/24;1 1/35;...`

Lời giải:

Các số hạng trong dãy được viết dưới dạng:

`4/3;9/8;16/15;25/24;36/35;...` hay `2^2/(1.3);3^2/2.4;4^2/3.5;5^2/4.6;6^2/5.7;...`

Theo quy luật trên, số hạng thứ `98` của dãy là `99^2/98.100`

Như vậy ta cần tính: `A=2^2/(1.3) . 3^2/2.4 . 4^2/3.5 . 5^2/4.6 . 6^2/5.7.... 98^2/97.99 . 99^2/98.100`

Để dễ rút gọn ta viết tử thành `(2.3.4....98.99).(2.3.4....98.99)`

Và mẫu thành `(1.2.3.4....97.98).(3.4.5....99.100)`

Khi đó: `A=2^2/(1.3) . 3^2/2.4 . 4^2/3.5 . 5^2/4.6 . 6^2/5.7.... 98^2/97.99 . 99^2/98.100`

`=((2.3.4....98.99).(2.3.4....98.99))/((1.2.3.4....97.98).(3.4.5....99.100))`

`=99/1 . 2/100=99/50`

Bài tập `4`: Tính giá trị biểu thức `M=(1+1/3+1/5+...+1/95+1/97+1/99)/(1/1.99 + 1/3.97 + 1/5.95 + ...+ 1/95.5+ 1/97.3 + 1/99.1)`

Lời giải: 

Đặt: `A=1+1/3+1/5+...+1/95+1/97+1/99`

        `B=1/1.99 + 1/3.97 + 1/5.95 + ...+ 1/95.5+ 1/97.3 + 1/99.1`

Ghép các phân số ở biểu thức `A` thành từng cặp để mẫu chung giống mẫu của các phân số tương ứng trong biểu thức `B`.

Sau đó biến đổi biểu thức `A` bằng cách cộng từng cặp các phân số cách đều hai đầu ta được:

`A=1+1/3+1/5+...+1/95+1/97+1/99`

`=(1+1/99)+(1/3 + 1/97)+...+(1/49+1/51)`

`=100/1.99 + 100/3.97 + ...+ 100/49.51`

`=100.(1/1.99 + 1/3.97 + ...+ 1/49.51)`

`B=1/1.99 + 1/3.97 + 1/5.95 + ...+ 1/95.5+ 1/97.3 + 1/99.1`

`=(1/99.1 + 1/1.99) + (1/3.97+1/97.3)+...+(1/49.51 + 1/51.49)`

`=2/1.99 + 2/3.97 + ...+2/49.51`

`=2(1/1.99 + 1/3.97 + ...+1/49.51)`

Do đó: `M=A/B=(100(1/1.99 + 1/3.97 + ...+1/49.51))/(2(1/1.99 + 1/3.97 + ...+1/49.51))=100/2=50`

2. Bài tập tự luyện

Bài `1.` Tính cách tổng sau:

`A=1/1.2 + 1/2.3 + 1/3.4 + ... +1/100.101`

`B=4/3.7+ 4/7.11 + 4/11.15 + ...+ 4/107.111`

`C=3^2/8.11 + 3^2/11.14 + 3^2/14.17+...+ 3^2/197.200`

`D=2/15 + 2/35+2/63+...+2/399`

Bài `2.` Tính các tổng sau:

`E=5/25.27+5/27.29+5/29.31+...+5/72.75`

`F=6/2.9 + 6/9.16 + 6/16.23 + ...+6/107.114`

`G=15/90.93 + 15/93.96 + 15/96.99+...+15/141.144`

`H=11/5 + 11/45 + 11/117+...+11/9797`

`M=1/15+1/21+1/28+...+1/190`

Bài `3.` Tìm `x` biết:

`a)` `x:(2/4.5 + 2/5.6 + 2/6.7 + ...+2/15.16)=4`

`b)` `1/1.6 + 1/6.11 + 1/11.16+...+1/(x.(x+5)) = 26/131`

Bài `4.` 

`a)` Tính nhanh `A=1/3 + 1/3^2+1/3^3+...+1/3^8`

`b)` Cho `B=1/2 + 1/2^2 +1/2^3+...+1/2^2019`. So sánh `B` với `1`

Bài `5.` Tính nhanh

`A=3/4 . 8/9 . 15/ 16 .... 99/100`

`B=(1-1/5)(1-1/6)(1-1/7)....(1-1/20)`

`C=(1+1/1.3)(1+1/2.4)(1+1/3.5)....(1+1/99.101)`

Bài `6.` Tính giá trị biểu thức:

`H=(1/2+1/3+1/4+...+1/100)/(99/1+98/2+97/3+...+1/99)`

`K=(1/2+1/4+1/6+...+1/96+1/98+1/100)/(1/2.100 + 1/4.98 + 1/6.96+...+1/96.6 + 1/98.4 + 1/100.2)`

Các bạn học sinh có thể xem đáp án các bài tập tự luyện tại đây nhé:

https://onthi123.vn/mot-so-bai-toan-ve-day-cac-phan-so-viet-theo-quy-luat